This week we will look at

Statement

This problem is generally quite hard so we look at the limited problem.

Statement

Theory

Solving 2-SAT problem

Simplifying the problem

First we simplify the input by getting rid of forced decisions. We do this by repeatedly looking for unit clauses with 1 literal and reducing the problem by removing this variable.

1. Take a unit clause, say literal $a_i$,
2. If the unit clause $\overline{a_i}$ exists output then no solution exists,
3. Satisfy it, set $a_i = T$,
   1. If a_i = x, then x = T, or
   2. If a_i = \overline{x} then x = F.
4. Remove clauses containing $a_i$ and drop $\overline{a_i}$ from clauses.
5. Let $f'$ be the resulting formula.

We can repeat this until either:

• we find an issue,
• the formula becomes empty and we have an assignment, or
• the output formula only has clauses with 2 variable.

Forming a graph

We can now assume our formula has all clauses of size 2, it will have $n$ variables $x_i$ and $m$ clauses $c_i = \alpha_i \lor \beta_i$ where $\alpha_i, \beta_i \in \{x_i, \overline{x_i} \vert 1 \leq i \leq n\}$. We want to form a directed graph $D = (V,E)$ to represent this problem.

• $V = \{x_i, \overline{x_i} \vert 1 \leq i \leq n\}$, and
• $E = \{(\overline{\alpha_i}, \beta_i), (\overline{\beta_i}, \alpha_i) \vert 1 \leq i \leq m\}$.

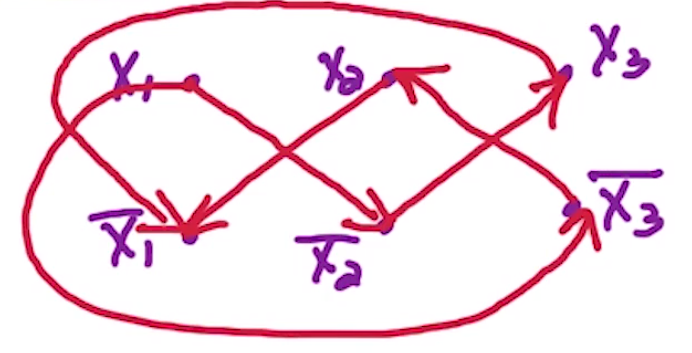
The intuition behind this graph is that for a clause $(\alpha \lor \beta)$ if $\overline{\alpha}$ then we will need $\beta$ to be true for a correct allocation for $f$, similarly with $\overline{\beta}$ we would need $\alpha$.

This logic extends out to paths.

Proof

Prove this by induction on the length of path.

Suppose the path is of length 1, i.e. $(a, b) \in E$. Therefore there is a clause $\overline{a} \lor b$ or $b \lor \overline{a}$, so if $a$ is true then $b$ needs to be true.

Suppose it is true for a path of length less than $k$.

Suppose we have a path of length $k>1$ $p (c,b)$ where $p$ is a path from $a$ to $c$ of length $k-1$.

By the induction hypothesis if $a$ is true then $c$ must be true.

As $(c,b) \in E$ we have a clause $\overline{c} \lor b$ or $b \lor \overline{c}$. As $c$ is true for this assignment to satisfy $f$ we need $b$ to be true.

Therefore by induction we have the statement holds for all length paths.

$\square$

This gives us an easy check for if $f$ is not satisfiable.

Proof

This means there is a path from $x_i$ to $\overline{x_i}$ and $\overline{x_i}$ to $x_i$.

From the lemma above if $x_i$ is true we would require $\overline{x_i}$ to be true also for an assignment to satisfy $f$. Similarly if $x_i$ then we need $\overline{x_i}$ to be true.

This is contradictory and so no such assignment exists.

$\square$

It would be useful to have the complement statement. Which turns out to be true but requires a lot more effort to prove.

To prove this lets examine the structure of the graph.

Proof

Let $(x_1, x_2) (x_2, x_3) \ldots (x_{n-1}, x_n)$ be a path from $x_1$ to $x_n$.

Note the edge $(x_{i}, x_{i+1})$ comes from the clause $\overline{x_i} \lor x_{i+1}$ or $x_{i+1} \lor \overline{x_i}$ however both these clauses give rise to the edge $(\overline{x_{i+1}}, \overline{x_i})$.

Therefore we have the path $(\overline{x_n}, \overline{x_{n-1}}) (\overline{x_{n-1}}, \overline{x_{n-2}}) \ldots (\overline{x_2}, \overline{x_1})$ which is exactly the path from $\overline{x_n}$ to $\overline{x_1}$.

Then if this path were from $a$ to $b$ this would give us a path to $\overline{b}$ to $\overline{a}$.

Similarly if this were a path from $\overline{b}$ to $\overline{a}$ we would get a path from $a$ to $b$.

This proves the required statement. $\square$

This means in $G$ it is meaningful to talk about complement paths. i.e. if $p_{a,b}$ is a path in $G$ from $a$ to $b$ then $\overline{p_{a,b}}$ is the complement path from $\overline{b}$ to $\overline{a}$ that we will refer to as $p_{\overline{b}, \overline{a}} := \overline{p_{a,b}}$.

This actually gives us quite a neat corollary.

Proof

For any two $s_1, s_2 \in S$ there exists a path $p_{1,2}$ and $p_{2,1}$ connecting $s_1$ to $s_2$ and $s_2$ to $s_1$.

By the Lemma above $\overline{p_{1,2}}$ and $\overline{p_{2,1}}$ connects $\overline{s_2}$ to $\overline{s_1}$ and $\overline{s_1}$ to $\overline{s_2}$. Showing that $\overline{s_1}$ and $\overline{s_2}$ are strongly connected to one another.

Equally if $\overline{t} \in V$ is strongly connected to $\overline{s} \in \overline{S}$ via paths $\overline{p_{t,s}}$ and $\overline{p_{s,t}}$ then $p_{t,s}$ and $p_{s,t}$ strongly connect $t$ to $s$ giving $t \in S$.

Therefore $\overline{S}$ is a strongly connected component of $G$.

$\square$

This this actually extends further.

Proof

Let $S$ be a strongly connected component in the strongly connected component graph.

From the Corollary above we know $\overline{S}$ is a strongly connected component.

$\Rightarrow$

Let $S$ be a sink.

Let $p_{t, \overline{s}}$ be a path from $t \in V$ to $\overline{s} \in \overline{S}$.

Note $\overline{p_{t,\overline{s}}} = p_{s, \overline{t}}$ is a path from $s \in S$ to $\overline{t} \in V$ from the lemma above.

However as $S$ is a sink $\overline{t} \in S$ as the only paths starting at $S$ have to end there.

This gives that $t \in \overline{S}$ and the only paths into $\overline{S}$ start at $\overline{S}$ making it a source.

$\Leftarrow$

Let $\overline{S}$ be a source.

Let $p_{s, t}$ be a path from $s \in S$ to $t \in V$.

Note $\overline{p_{s,t}} = p_{\overline{t}, \overline{s}}$ is a path from $\overline{t} \in V$ to $\overline{s} \in \overline{S}$ from the lemma above.

However as $\overline{S}$ is a source $\overline{t} \in \overline{S}$ as the only paths into $\overline{S}$ have to start there.

This gives $t \in S$ and the only paths out of $S$ have to start in $S$ making it a sink.

$\square$

Using this we can prove.

Proof

Find the strongly connected component graph of $G$, $SCC(G)$.

We can pair the strongly connected components $S$ with $\overline{S}$. From the assumption of the lemma $S \not = \overline{S}$ for any strongly connected component.

To satisfy $f$ we need to find a True/False allocation to the strongly connected components such that:

• If $S$ is True then $\overline{S}$ is False, and
• If $S$ is True and it has a path to $T$ then $T$ is True.

To do this find a sink $S$ in $SCC(G)$ then we know $\overline{S}$ is a source. Assign $S$ to be True and $\overline{S}$ to be false.

Then remove $S$ and $\overline{S}$ from $SCC(G)$ and repeat.

This assignment satisfies the first property as when we set $S$ to True we set $\overline{S}$ to false.

This assignment satisfies the second property if $S$ is True and has a path to $T$. The $T$ was removed before $S$.

As $T$ has a path from $S$ it couldn’t have been a source, so must have been a sink. It therefore was allocated True.

So this allocation satisfies $f$ and it is satisfiable.

$\square$

This is exactly how our algorithm will go as well.

2-Sat algorithm

Without the simplification step we have the following algorithm

2SAT-simplified(f):
	Input: 2-SAT problem on n variables with m clauses where each clause has 2 variables.
	Output: Assignment from n variables satisfying f or saying no assignment is possible.
1. Construct graph G for f'.
2. Run SCC algorithm on S.
3. If any variable and its complement are in the same SCC return no assignment possible.
4. While still SCC left.
	1. Take sink SCC S,
	2. Set the clauses in S to true (and thier complements to false)
	3. Remove S & \overline{S}
7. Return assignment.

Constructing the graph takes $O(m)$ steps. Then running the SCC algorithm takes $O(n + m)$. Lastly filtering the strongly connected components takes at most $O(n)$ steps as we have to run through the list of variables and their complements. (Note the ordering SCC algorithm algorithm returns in is a topologically sort so it isn’t hard to identify sink components.)

All together this runs in $O(n + m)$ time. However the algorithm with the above simplification

2SAT(f):
	Input: 2-SAT problem on n variables with m clauses.
	Output: Assignment from n variables satisfying f or saying no assignment is possible.
1. Set f' = f
2. While f' has a unit clauses:
	1. Find a unit clause c.
	2. Assign c to True.
	3. If \overline{c} is a unity clause return no assignment possible.
	4. Remove clauses with c in and remove occurances of \overline{c}.
	5. Set this new statement to f'.
3. Construct graph G for f'.
4. Run SCC algorithm on S.
5. If any variable and its complement are in the same SCC return no assignment possible.
6. While still SCC left.
	1. Take sink SCC S,
	2. Set the clauses in S to true (and thier complements to false)
	3. Remove S & \overline{S}
7. Return assignment.

This looks like it takes $O(nm)$ time to simplify the algorithm. However, clever use of data structures can help us here.

simplify(f)
	Input: 2-sat potenially with unit litterals.
	Output: Either there is not solution to the input, or a 2-sat that has 2 variables in every clause and a partial solution to f.
1. Define U and C_v to be list where v in variables
2. for clause c in f (let c be some positional variable not the expression of the clause)
	2.1. if c unit so f(c) = x, not x
		2.1.1. add c to C_x (position)
		2.1.2. add x or not x to U (variable)
	2.2. else f(c) = (not) x or (not) y
		2.2.1. add c to C_x and C_y (position)
3. Let f' = f (pick a data structure where looking up clauses is O(1) from a positional arguement)
4. While U not empty
	4.1. x or not x (set this to X) be the next value in U - removing it
		in the process
	4.2. if C_x exists
		4.2.1. for c in C_x
			4.2.1.1. if f'(c) contains X in f' remove it from f'.
			4.2.1.2. if f'(c) is (not X) in f' output that f has no solution
			4.2.1.3. if f'(c) contains not X (so f'(c) = not X or Y)
				4.2.1.3.1. remove not X from f'(c)
				4.2.1.3.2. append Y to U
		4.2.2. set X to true in our partial solution
		4.2.3. Remove C_x
5. output f' and partial solution to f.

This takes $O(n + m)$ as we have $n$ lists we make and we visit each clause at most 3 times during the algorithm.

We can instead expand the problem for a simpler algorithm. The pseudo code is below.

2-SAT algorithm using SCC

The solution to $f'$ is valid for $f$ - as for any unit clause in $f$ $u_i$ we have $(u_i \lor Y) \land (u_i \lor \overline{Y})$ meaning regardless of the value of $Y$ $u_i$ has to be true. Then correctness follows from the proof above.

This also has run time $O(n + m)$. The simplification takes $O(m)$ time which produces a problem with $n+1$ variables and at most $2m$ clauses. So from above this solves in $O(n+1 + 2m) = O(n + m)$. Giving an overall run time of $O(n + m)$.

Run time