Complexity classes

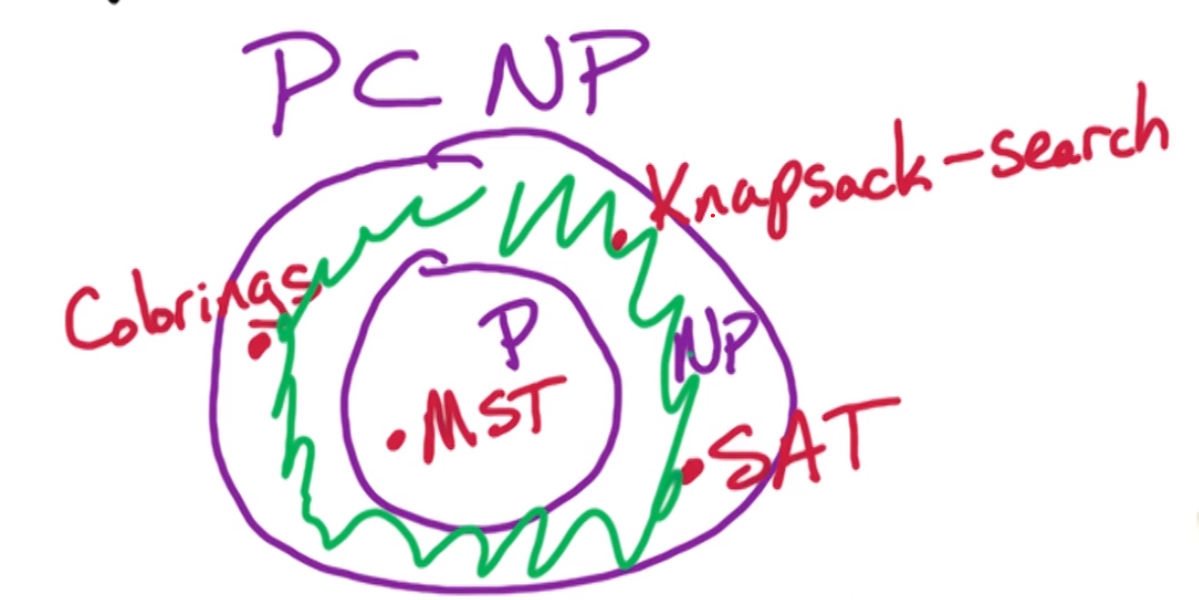
Nondeterministic Polynomial time (NP)

In this class we use the search problem definition.

Search problems

Note here we have.

Statement

There is an open problem.

P equals NP or P not equals NP

Satisfiability

SAT problem

The Satisfiability problem is in NP

k-colourings problem

Statement

The k-colourings problem is in NP

MST

MST

Minimum Spanning Tree problem is in NP

This proof was relatively easy as MST is a polynomial time problem. This is shown by what is above and Kruskal’s algorithm.

Knapsack problem

Statement

Whilst the Knapsack problem is of the correct form to be a search problem we can’t currently check if a solution is correct in polynomial time. Therefore the Knapsack problem isn’t known to be in NP.

Similarly we say that the Knapsack problem isn’t known to be in polynomial time either.

We say it isn’t known to be as there might be a super clever algorithm that happens to solve the Knapsack problem in polynomial time.

However, there is a variant of the problem that is in NP.

Statement

Here instead of having to check if a solution is maximal we can instead just check if it has enough value.

Knapsack-search is NP

Polynomial time and Nondeterministic Polynomial time

Note that NP isn’t Not Polynomial time. In fact we have the following result.

Polynomial time is a subset of NP-complete

The question is, are there problems that are in NP but are not in P?

NP-complete

If P not equal to NP then we would have a problem in NP that didn’t lie in P. Therefore the green region above would be non-empty.

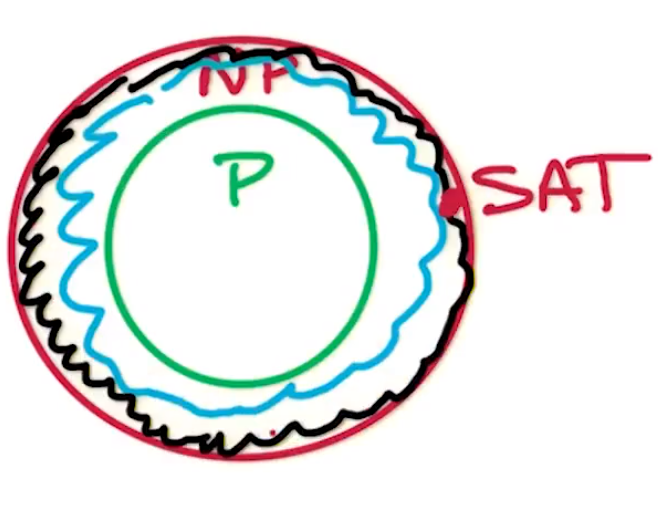
Therefore lets look at the hardest problems in NP.

NP-hard

We define a many-one reduction as bellow.

Many-one reduction

However, we want to look at the hardest problems in NP.

NP-Complete

A classic NP-Complete problem is the SAT problem.

Reductions functionally

To show a many-one reduction from $A$ to $B$ you need to construct $f$ a way to transform an instance of problem $A$ into some input to the problem $B$. This needs to be done in polynomial time. Then the solution from solving $f(I)$ in problem $B$ should relate back to the solution of problem $A$. Either you should construct $h$ a way to transform the solution from problem $B$ into a solution to problem $A$ or forward on the fact that no solution can exist.

Therefore to show $A$ reduces to $B$ we need:

• Define $f$: Show how an instance of problem $A$ can be converted into an instance of problem $B$ in polynomial time.
• Define $h$: Show how a solution to the problem $B$ can be converted into a solution to problem $A$ in polynomial time.
• Proof: Show that a solution for $B$ exists if and only if a solution to $A$ exists.

Showing NP-Complete

To show a problem $A$ is NP-Complete need to show

• $A$ is in NP, and
• $A$ is NP-hard.

Generically showing $A$ is NP-hard, is ironically quite hard. However we get around this by having some NP-complete problems already, such as the SAT problem. Then to show $A$ is NP-hard we just need to show another NP-Complete problem reduces to it. So functionally we show:

• $A$ is NP, and
• there is some NP-complete problem $B$ that reduces to $A$.

Practice problems

From Algorithms by S. Dasgupta, C. Papadimitriou, and U. Vazirani.